MTG - Multi-scale Tree Graph

Overview

openalea.mtg.mtg.MTG(filename='', has_date=False)[source]

A Multiscale Tree Graph (MTG) class.

MTGs describe tree structures at different levels of details, named scales. For example, a botanist can described plants at different scales :

  • at scale 0, the whole scene.

  • at scale 1, the individual plants.

  • at scale 2, the axes of each plants.

  • at scale 3, the growth units of each axis, and so on.

Each scale can have a label, e.g. :

  • scale 1 : P(lant)

  • scale 2 : A(xis)

  • sclae 3 : U(nit of growth)

Compared to a classical tree, complex() can be seen as parent() and components() as children(). An element at scale() N belongs to a complex() at scale() N-1 and has components() at scale N+1:

  • /P/A/U (decomposition is noted using “/”)

Each scale is itself described as a tree or a forest (i.e. set of trees), e.g.:

  • /P1/P2/P3

  • A1+A2<A3

  • …

Iterating over vertices

MTG.root

Return the tree root.

MTG.vertices([scale])

Return a list of the vertices contained in an MTG.

MTG.nb_vertices([scale])

Returns the number of vertices.

MTG.parent(vtx_id)

Return the parent of vtx_id.

MTG.children(vtx_id)

returns a vertex iterator

MTG.nb_children(vtx_id)

returns the number of children

MTG.siblings(vtx_id)

returns an iterator of vtx_id siblings.

MTG.nb_siblings(vtx_id)

returns the number of siblings

MTG.roots([scale])

Returns a list of the roots of the tree graphs at a given scale.

MTG.complex(vtx_id)

Returns the complex of vtx_id.

MTG.components(vid)

returns the components of a vertex

MTG.nb_components(vid)

returns the number of components

MTG.complex_at_scale(vtx_id, scale)

Returns the complex of vtx_id at scale scale.

MTG.components_at_scale(vid, scale)

returns a vertex iterator

Adding and removing vertices

MTG.__init__([filename, has_date])

Create a new MTG object.

MTG.add_child(parent[, child])

Add a child to a parent.

MTG.insert_parent(vtx_id[, parent_id])

Insert parent_id between vtx_id and its actual parent.

MTG.insert_sibling(vtx_id1[, vtx_id2])

Insert a sibling of vtk_id1.

MTG.add_component(complex_id[, component_id])

Add a component at the end of the components

MTG.add_child_and_complex(parent[, child, ...])

Add a child at the end of children that belong to an other complex.

MTG.add_child_tree(parent, tree)

Add a tree after the children of the parent vertex.

MTG.clear()

Remove all vertices and edges from the MTG.

Some usefull functions

simple_tree(tree, vtx_id[, nb_children, ...])

Generate and add a regular tree to an existing one at a given vertex.

random_tree(mtg, root[, nb_children, ...])

Generate and add a random tree to an existing one.

random_mtg(tree, nb_scales)

Convert a tree into an MTG of nb_scales.

colored_tree(tree, colors)

Compute a mtg from a tree and the list of vertices to be quotiented.

display_tree(tree, vid[, tab, labels, edge_type])

Display a tree structure.

display_mtg(mtg, vid)

Display an MTG

All

class openalea.mtg.mtg.MTG(filename='', has_date=False)[source]

Bases: PropertyTree

A Multiscale Tree Graph (MTG) class.

MTGs describe tree structures at different levels of details, named scales. For example, a botanist can described plants at different scales :

  • at scale 0, the whole scene.

  • at scale 1, the individual plants.

  • at scale 2, the axes of each plants.

  • at scale 3, the growth units of each axis, and so on.

Each scale can have a label, e.g. :

  • scale 1 : P(lant)

  • scale 2 : A(xis)

  • sclae 3 : U(nit of growth)

Compared to a classical tree, complex() can be seen as parent() and components() as children(). An element at scale() N belongs to a complex() at scale() N-1 and has components() at scale N+1:

  • /P/A/U (decomposition is noted using “/”)

Each scale is itself described as a tree or a forest (i.e. set of trees), e.g.:

  • /P1/P2/P3

  • A1+A2<A3

  • …

AlgHeight(v1, v2)[source]

Algebraic value defining the number of components between two components.

This function is similar to function Height(v1, v2) : it returns the number of components between two components, at the same scale, but takes into account the order of vertices v1 and v2.

The result is positive if v1 is an ancestor of v2, and negative if v2 is an ancestor of v1.

Usage:

AlgHeight(v1, v2)
Parameters:

  • v1 (int) : vertex of the active MTG.

  • v2 (int) : vertex of the active MTG.

Returns:

int

If v1 is not an ancestor of v2 (or vise versa), or if v1 and v2 are not defined at the same scale, an error value None is returned.

See also

MTG(), Rank(), Order(), Height(), EdgeType(), AlgOrder(), AlgRank().

AlgOrder(v1, v2)[source]

Algebraic value defining the relative order of one vertex with respect to another one.

This function is similar to function Order(v1, v2) : it returns the number of +-type edges between two components, at the same scale, but takes into account the order of vertices v1 and v2.

The result is positive if v1 is an ancestor of v2, and negative if v2 is an ancestor of v1.

Usage:

AlgOrder(v1, v2)
Parameters:

  • v1 (int) : vertex of the active MTG.

  • v2 (int) : vertex of the active MTG.

Returns:

int

If v1 is not an ancestor of v2 (or vise versa), or if v1 and v2 are not defined at the same scale, an error value None is returned.

See also

MTG(), Rank(), Order(), Height(), EdgeType(), AlgHeight(), AlgRank().

AlgRank(v1, v2)[source]

Algebraic value defining the relative rank of one vertex with respect to another one.

This function is similar to function Rank(v1, v2) : it returns the number of <-type edges between two components, at the same scale, but takes into account the order of vertices v1 and v2.

The result is positive if v1 is an ancestor of v2, and negative if v2 is an ancestor of v1.

Usage:

AlgRank(v1, v2)
Parameters:

  • v1 (int) : vertex of the active MTG.

  • v2 (int) : vertex of the active MTG.

Returns:

int

If v1 is not an ancestor of v2 (or vise versa), or if v1 and v2 are not defined at the same scale, an error value None is returned.

See also

MTG(), Rank(), Order(), Height(), EdgeType(), AlgHeight(), AlgOrder().

Ancestors(v, EdgeType='*', RestrictedTo='NoRestriction', ContainedIn=None)[source]

Array of all vertices which are ancestors of a given vertex

This function returns the array of vertices which are located before the vertex passed as an argument. These vertices are defined at the same scale as v. The array starts by v, then contains the vertices on the path from v back to the root (in this order) and finishes by the tree root.

Note

The anscestor array always contains at least the argument vertex v.

Usage:

g.Ancestors(v)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • RestrictedTo (str): cf. Father

  • ContainedIn (int): cf. Father

  • EdgeType (str): cf. Father

Returns:

list of vertices’s id (int)

Examples:

>>> v # prints vertex v
78
>>> g.Ancestors(v) # set of ancestors of v at the same scale
[78,45,32,10,4]
>>> list(reversed(g.Ancestors(v))) # To get the vertices in the order from the root to the vertex v
[4,10,32,45,78]

See also

MTG(), Descendants().

Axis(v, Scale=-1)[source]

Array of vertices constituting a botanical axis

An axis is a maximal sequence of vertices connected by ‘<’-type edges. Axis return the array of vertices representing the botanical axis which the argument v belongs to. The optional argument enables the user to choose the scale at which the axis decomposition is required.

Usage:

Axis(v)
Axis(v, Scale=s)
Parameters:

  • v (int) : Vertex of the active MTG

Optional Parameters:

  • Scale (str): scale at which the axis components are required.

Returns:

list of vertices ids

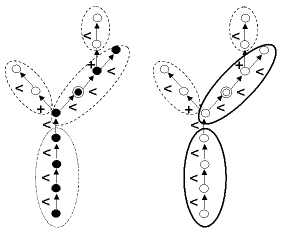
../_images/mtg_axis.png

See also

MTG(), Path(), Ancestors().

Class(vid)

Class of a vertex.

The Class of a vertex are the first characters of the label. The label of a vertex is the string defined by the concatenation of the class and its index.

The label thus provides general information about a vertex and enable to encode the plant components.

The class_name may be not defined. Then, an empty string is returned.

Usage:
>>> g.class_name(1)
Parameters:

  • vid (int)

Returns:

The class name of the vertex (str).

See also

MTG(), openalea.mtg.aml.Index(), openalea.mtg.aml.Class()

ClassScale(c)[source]

Scale at which appears a given class of vertex

Every vertex is associated with a unique class. Vertices from a given class only appear at a given scale which can be retrieved using this function.

Usage:

ClassScale(c)
Parameters:

  • c (str) : symbol of the considered class

Returns:

int

See also

MTG(), Class(), Scale(), Index().

Complex(v, Scale=-1)[source]

Complex of a vertex.

Returns the complex of v. The complex of a vertex v has a scale lower than v : Scale(v) - 1. In a MTG, every vertex except for the MTG root (cf. MTGRoot), has a uniq complex. None is returned if the argument is the MTG Root or if the vertex is undefined.

Usage:

g.Complex(v)
g.Complex(v, Scale=2)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • Scale (int) : scale of the complex

Returns:

Returns vertex’s id (int)

Details:

When a scale different form Scale(v)-1 is specified using the optional parameter Scale, this scale must be lower than that of the vertex argument.

Todo

Complex(v, Scale=10) returns v why ? is this expected

See also

MTG(), Components().

ComponentRoots(v, Scale=-1)[source]

Set of roots of the tree graphs that compose a vertex

In a MTG, a vertex may have be decomposed into components. Some of these components are connected to each other, while other are not. In the most general case, the components of a vertex are organized into several tree-graphs. This is for example the case of a MTG containing the description of several plants: the MTG root vertex can be decomposed into tree graphs (not connected) that represent the different plants. This function returns the set of roots of these tree graphs at scale Scale(v)+1. The order of these roots is not significant.

When a scale different from Scale(v)+1 is specified using the optional argument Scale(), this scale must be greater than that of the vertex argument.

Usage:

g.ComponentRoots(v)
g.ComponentRoots(v, Scale=s)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • Scale (str): scale of the component roots.

Returns:

list of vertices’s id (int)

Examples:

>>> v=g.MTGRoot() # global MTG root
0
>>> g.ComponentRoots(v) # set of first vertices at scale 1
[1,34,76,100,199,255]
>>> g.ComponentRoots(v, Scale=2) # set of first vertices at scale 2
[2,35,77,101,200,256]
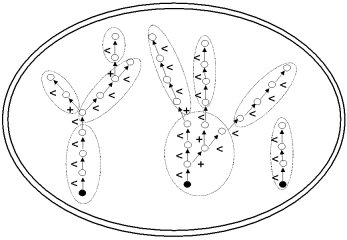
../_images/mtg_componentroots.png

See also

MTG(), Components(), Trunk().

Components(v, Scale=-1)[source]

Set of components of a vertex.

The set of components of a vertex is returned as a list of vertices. If s defines the scale of v, components are defined at scale s + 1. The array is empty if the vertex has no components. The order of the components in the array is not significant.

When a scale is specified using optional argument :arg:Scale, it must be necessarily greater than the scale of the argument.

Usage:

Components(v)
Components(v, Scale=2)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • Scale (int) : scale of the components.

Returns:

list of int

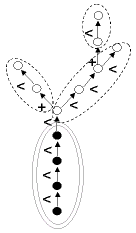
../_images/mtg_components.png

See also

MTG(), Complex().

Defined(vid)[source]

Test whether a given vertex belongs to the active MTG.

Usage:

Defined(v)
Parameters:

  • v (int) : vertex of the active MTG

Returns:

True or False

See also

MTG().

Descendants(v, EdgeType='*', RestrictedTo='NoRestriction', ContainedIn=None)[source]

Set of vertices in the branching system borne by a vertex.

This function returns the set of descendants of its argument as an array of vertices. The array thus consists of all the vertices, at the same scale as v, that belong to the branching system starting at v. The order of the vertices in the array is not significant.

Note

The argument always belongs to the set of its descendants.

Usage:

g.Descendants(v)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • RestrictedTo (str): cf. Father

  • ContainedIn (int): cf. Father

  • EdgeType (str): cf. Father

Returns:

list of int.

Examples:

>>> v
78
>>> g.Sons(v) # set of sons of v
[78,99,101]
>>> g.Descendants(v) # set of descendants of v
[78,99,101,121,133,135,156,171,190]
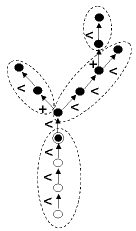
../_images/mtg_descendants.png

See also

MTG(), Ancestors().

EdgeType(v1, v2)[source]

Type of connection between two vertices.

Returns the symbol of the type of connection between two vertices (either < or +). If the vertices are not connected, None is returned.

Usage:

EdgeType(v1, v2)
Parameters:

  • v1 (int) : vertex of the active MTG

  • v2 (int) : vertex of the active MTG

Returns:

‘<’ (successor), ‘+’ (branching) or None

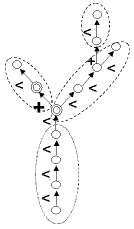
../_images/mtg_edgetype.png

See also

MTG(), Sons(), Father().

Extremities(v, RestrictedTo='NoRestriction', ContainedIn=None)[source]

Set of vertices that are the extremities of the branching system born by a given vertex.

This function returns the extremities of the branching system defined by the argument as a list of vertices. These vertices have the same scale as v and their order in the list is not signifiant. The result is always a non empty array.

Usage:

Extremities(v)
Properties:

  • v (int) : vertex of the active MTG

Optional Parameters:
Returns:

list of vertices’s id (int)

Examples:

>>> g.Descendants(v)
[3, 45, 47, 78, 102]
>>> g.Extremities(v)
[47, 102]

See also

MTG(), Descendants(), Root(), MTGRoot().

Father(v, EdgeType='*', RestrictedTo='NoRestriction', ContainedIn=None, Scale=-1)[source]

Topological father of a given vertex.

Returns the topological father of a given vertex. And None if the father does not exist. If the argument is not a valid vertex, None is returned.

Usage:

g.Father(v)
g.Father(v, EdgeType='<')
g.Father(v, RestrictedTo='SameComplex')
g.Father(v, ContainedIn=complex_id)
g.Father(v, Scale=s)
Parameters:

v (int) : vertex of the active MTG

Optional Parameters:

If no optional argument is specified, the function returns the topological father of the argument (vertex that bears or precedes to the vertex passed as an argument).

It may be usefull in some cases to consider that the function only applies to a subpart of the MTG (e.g. an axis).

The following options enables us to specify such restrictions:

  • EdgeType (str) : filter on the type of edge that connect the vertex to its father.

    Values can be ‘<’, ‘+’, and ‘*’. Values ‘*’ means both ‘<’ and ‘+’. Only the vertex connected with the specified type of edge will be considered.

  • RestrictedTo (str) : filter defining a subpart of the MTG where the father must be considered. If the father is actually outside this subpart, the result is None. Possible subparts are defined using keywords in [‘SameComplex’, ‘SameAxis’, ‘NoRestriction’].

    For instance, if RestrictedTo is set to ‘SameComplex’, Father(v)() returns a defined vertex only if the father f of v existsin the MTG and if v and f have the same complex.

  • ContainedIn (int) : filter defining a subpart of the MTG where the father must be considered. If the father is actually outside this subpart, the result is None.

    In this case, the subpart of the MTG is made of the vertices that composed composite_id (at any scale).

  • Scale (int) : the scale of the considered father. Returns the vertex from scale s which either bears and precedes the argument.

    The scale s can be lower than the argument’s (corresponding to a question such as ‘which axis bears the internode?’) or greater (e.g. ‘which internodes bears this annual shoot?’).

Returns:

the vertex id of the Father (int)

See also

MTG(), Defined(), Sons(), EdgeType(), Complex(), Components().

Height(v1, v2=None)[source]

Number of components existing between two components in a tree graph.

The height of a vertex (v2) with respect to another vertex (v1) is the number of edges (of either type ‘+’ or ‘<’) that must be crossed when going from v1 to v2 in the graph.

This is a non-negative integer. When the function has only one argument v1, the height of v1 correspond to the height of v1`with respect to the root of the branching system containing `v1.

Usage:

Height(v1)
Height(v1, v2)
Parameters:

  • v1 (int) : vertex of the active MTG

  • v2 (int) : vertex of the active MTG

Returns:

int

Note

When the function takes two arguments, the order of the arguments is not important provided that one is an ancestor of the other. When the order is relevant, use function AlgHeight.

See also

MTG(), Order(), Rank(), EdgeType(), AlgHeight(), AlgHeight(), AlgOrder().

Index(vid)

Index of a vertex

The Index of a vertex is a feature always defined and independent of time (like the index). It is represented by a non negative integer. The label of a vertex is the string defined by the concatenation of its class and its index. The label thus provides general information about a vertex and enables us to encode the plant components.

Label(vid)

Label of a vertex.

Usage:
>>> g.label(v)
Parameters:

  • vid (int) : vertex of the MTG

Returns:

The class and Index of the vertex (str).

See also

MTG(), index(), class_name()

Path(v1, v2)[source]

List of vertices defining the path between two vertices

This function returns the list of vertices defining the path between two vertices that are in an ancestor relationship. The vertex v1 must be an ancestor of vertex v2. Otherwise, if both vertices are valid, then the empty array is returned and if at least one vertex is undefined, None is returned.

Usage:

g.Path(v1, v2)
Parameters:

  • v1 (int) : vertex of the active MTG

  • v2 (int) : vertex of the active MTG

Returns:

list of vertices’s id (int)

Examples:

>>> v # print the value of v
78
>>> g.Ancestors(v)
[78,45,32,10,4]
>>> g.Path(10,v)
[10,32,45,78]
>>> g.Path(9,v) # 9 is not an ancestor of 78
[]

Note

v1 can be equal to v2.

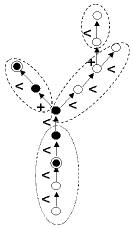
../_images/mtg_path.png

See also

MTG(), Axis(), Ancestors().

Predecessor(v, **kwds)[source]

Father of a vertex connected to it by a ‘<’ edge

This function is equivalent to Father(v, EdgeType-> ‘<’). It thus returns the father (at the same scale) of the argument if it is located in the same botanical. If it does not exist, None is returned.

Usage:

Predecessor(v)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • RestrictedTo (str): cf. Father

  • ContainedIn (int): cf. Father

Returns:

return the vertex id (int)

Examples:

>>> Predecessor(v)
7
>>> Father(v, EdgeType='+')
>>> Father(v, EdgeType-> '<')
7

See also

MTG(), Father(), Successor().

Rank(v1, v2=None)[source]

Rank of one vertex with respect to another one.

This function returns the number of consecutive ‘<’-type edges between two components, at the same scale, and does not take into account the order of vertices v1 and v2. The result is a non negative integer.

Usage:

Rank(v1)
Rank(v1, v2)
Parameters:

  • v1 (int) : vertex of the active MTG

  • v2 (int) : vertex of the active MTG

Returns:

int

If v1 is not an ancestor of v2 (or vise versa) within the same botanical axis, or if v1 and v2 are not defined at the same scale, an error value Undef id returned.

See also

MTG(), Order(), Height(), EdgeType(), AlgRank(), AlgHeight(), AlgOrder().

Root(v, RestrictedTo='*', ContainedIn=None)[source]

Root of the branching system containing a vertex

This function is equivalent to Ancestors(v, EdgeType=’<’)[-1]. It thus returns the root of the branching system containing the argument. This function never returns None.

Usage:

g.Root(v)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • RestrictedTo (str): cf. Father

  • ContainedIn (int): cf. Father

Returns:

return vertex’s id (int)

Examples:

>>> g.Ancestors(v) # set of ancestors of v
[102,78,35,33,24,12]
>>> g.Root(v) # root of the branching system containing v
12
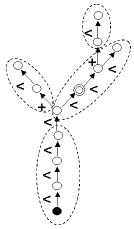
../_images/mtg_root.png

See also

MTG(), Extremities().

Scale(vid)

Returns the scale of a vertex.

All vertices should belong to a given scale.

Usage:

g.scale(vid)
Parameters:

  • vid (int) - vertex identifier.

Returns:

The scale of the vertex. It is a positive int in [0,g.max_scale()].

Sons(v, RestrictedTo='NoRestriction', EdgeType='*', Scale=-1, ContainedIn=None)[source]

Set of vertices born or preceded by a vertex

The set of sons of a given vertex is returned as an array of vertices. The order of the vertices in the array is not significant. The array can be empty if there are no son vertices.

Usage:

g.Sons(v)
g.Sons(v, EdgeType= '+')
g.Sons(v, Scale= 3)
Parameters:

  • v (int) : vertex of the active MTG

Optional Parameters:

  • RestrictedTo (str) : cf. Father()

  • ContainedIn (int) : cf. Father()

  • EdgeType (str) : filter on the type of sons.

  • Scale (int) : set the scale at which sons are considered.

Returns:

list(vid)

Details:

When the option EdgeType is applied, the function returns the set of sons that are connected to the argument with the specified type of relation.

Note

Sons(v, EdgeType= ‘<’) is not equivalent to Successor(v). The first function returns an array of vertices while the second function returns a vertex.

The returned vertices have the same scale as the argument. However, coarser or finer vertices can be obtained by specifying the optional argument Scale at which the sons are considered.

Examples:

>>> g.Sons(v)
[3,45,47,78,102]
>>>  g.Sons(v, EdgeType= '+') # set of vertices borne by v
[3,45,47,102]
>>>  g.Sons(v, EdgeType= '<') # set of successors of v on the same axis
[78]

See also

MTG(), Father(), Successor(), Descendants().

Successor(v, RestrictedTo='NoRestriction', ContainedIn=None)[source]

Vertex that is connected to a given vertex by a ‘<’ edge type (i.e. in the same botanical axis).

This function is equivalent to Sons(v, EdgeType=’<’)[0]. It returns the vertex that is connected to a given vertex by a ‘<’ edge type (i.e. in the same botanical axis). If many such vertices exist, an arbitrary one is returned by the function. If no such vertex exists, None is returned.

Usage:

g.Successor(v)
Parameters:

  • v1 (int) : vertex of the active MTG

Optional Parameters:

  • RestrictedTo (str): cf. Father

  • ContainedIn (int): cf. Father

Returns:

Returns vertex’s id (int)

Examples:

>>> g.Sons(v)
[3, 45, 47, 78, 102]
>>> g.Sons(v, EdgeType='+') # set of vertices borne by v
[3, 45, 47, 102]
>>> g.Sons(v, EdgeType-> '<') # set of successors of v
[78]
>>> g.Successor(v)
78

See also

MTG(), Sons(), Predecessor().

Trunk(v, Scale=-1)[source]

List of vertices constituting the bearing botanical axis of a branching system.

Trunk returns the list of vertices representing the botanical axis defined as the bearing axis of the whole branching system defined by v. The optional argument enables the user to choose the scale at which the trunk should be detailed.

Usage:

Trunk(v)
Trunk(v, Scale= s)
Parameters:

  • v (int) : Vertex of the active MTG.

Optional Parameters:

  • Scale (str): scale at which the axis components are required.

Returns:

list of vertices ids

Todo

check the usage of the optional argument Scale

See also

MTG(), Path(), Ancestors(), Axis().

VtxList(Scale=-1)[source]

Array of vertices contained in a MTG

The set of all vertices in the MTG() is returned as an array. Vertices from all scales are returned if no option is used. The order of the elements in this array is not significant.

Usage:

>>> VtxList()
>>> VtxList(Scale=2)
Optional Parameters:

  • Scale (int): used to select components at a particular scale.

Returns:

  • list of vid

Background:

MTGs()

See also

MTG(), scale(), Class(), index().

add_child(parent, child=None, **properties)[source]

Add a child to a parent. Child is appended to the parent’s child list.

Parameters:

  • parent (int) - The parent identifier.

  • child (int or None) - The child identifier. If None,

    an ID is generated.

Returns:

Identifier of the inserted vertex (child)

Returns Type:

int

add_child_and_complex(parent, child=None, complex=None, **properties)[source]

Add a child at the end of children that belong to an other complex.

Parameters:

  • parent: The parent identifier.

  • child: Set the child identifier to this value if defined.

  • complex: Set the complex identifier to this value if defined.

Returns:

(vid, vid): child and complex ids.

add_child_tree(parent, tree)

Add a tree after the children of the parent vertex. Complexity have to be O(1) if tree == sub_tree()

Parameters:

  • parent – vertex identifier

  • tree – a rooted tree

add_component(complex_id, component_id=None, **properties)[source]

Add a component at the end of the components

Parameters:

  • complex_id: The complex identifier.

  • component_id: Set the component identifier to this value if defined.

Returns:

The id of the new component or the component_id if given.

add_element(parent_id, edge_type='/', scale_id=None)[source]

Add an element to the graph, if vid is not provided create a new vid ??? .. warning: Not Implemented.

Parameters:

  • parent_id (int) - The id of the parent vertex

  • edge_type (str) - The type of relation:

    • “/” : component (default)

    • “+” : branch

    • “<” : successor.

  • scale_id (int) - The id of the scale in which to

    add the vertex.

Returns:

The vid of the created vertex

add_property(property_name)

Add a new map between vid and a data Do not fill this property for any vertex

children(vtx_id)

returns a vertex iterator

Parameters:

vtx_id – The vertex identifier.

Returns:

iter of vertex identifier

children_iter(vtx_id)

returns a vertex iterator

Parameters:

vtx_id – The vertex identifier.

Returns:

iter of vertex identifier

class_name(vid)[source]

Class of a vertex.

The Class of a vertex are the first characters of the label. The label of a vertex is the string defined by the concatenation of the class and its index.

The label thus provides general information about a vertex and enable to encode the plant components.

The class_name may be not defined. Then, an empty string is returned.

Usage:
>>> g.class_name(1)
Parameters:

  • vid (int)

Returns:

The class name of the vertex (str).

See also

MTG(), openalea.mtg.aml.Index(), openalea.mtg.aml.Class()

clear()[source]

Remove all vertices and edges from the MTG.

This also removes all vertex properties. Don’t change references to object such as internal dictionaries.

Example:
>>> g.clear()
>>> g.nb_vertices()
0
>>> len(g)
0
clear_properties(exclude=[])[source]

Remove all the properties of the MTG.

Example:
>>> g.clear_properties()
complex(vtx_id)[source]

Returns the complex of vtx_id.

Parameters:

  • vtx_id (int) - The vertex identifier.

Returns:

complex identifier or None if vtx_id has no parent.

Return Type:

int

complex_at_scale(vtx_id, scale)[source]

Returns the complex of vtx_id at scale scale.

Parameters:

  • vtx_id: The vertex identifier.

  • scale: The scale identifier.

Returns:

vertex identifier

Returns Type:

int

component_roots(vtx_id)[source]

Return the set of roots of the tree graphs that compose a vertex.

component_roots_at_scale(vtx_id, scale)[source]

Return the list of roots of the tree graphs that compose a vertex.

component_roots_at_scale_iter(vtx_id, scale)[source]

Return the set of roots of the tree graphs that compose a vertex.

component_roots_iter(vtx_id)[source]

Return an iterator of the roots of the tree graphs that compose a vertex.

components(vid)[source]

returns the components of a vertex

Parameters:

vid – The vertex identifier.

Returns:

list of vertex identifier

components_at_scale(vid, scale)[source]

returns a vertex iterator

Parameters:

  • vid: The vertex identifier.

Returns:

iter of vertex identifier

components_at_scale_iter(vid, scale)[source]

returns a vertex iterator

Parameters:

  • vid: The vertex identifier.

Returns:

iter of vertex identifier

components_iter(vid)[source]

returns a vertex iterator

Parameters:

vid – The vertex identifier.

Returns:

iter of vertex identifier

copy()[source]

Return a copy of the graph.

Returns:

  • g (MTG) - A copy of the MTG

display(max_scale=0, display_id=True, display_scale=False, nb_tab=12, **kwds)[source]

Print an MTG on the console.

Optional Parameters:

  • max_scale: do not print vertices of scale greater than max_scale

  • display_id: display the vid of the vertices

  • display_scale: display the scale of the vertices

  • nb_tab: display the MTG using nb_tab columns

edge_type(vid)[source]

Type of the edge between a vertex and its parent.

The different values are ‘<’ for successor, and ‘+’ for ramification.

edges(scale=-1)[source]
Parameters:

  • scale (int) - Scale at which to iterate.

Returns:

Iterator on the edges of the MTG at a given scale or on all edges if scale < 0.

Returns Type:

iter

get_root()

Return the tree root.

Returns:

vertex identifier

get_vertex_property(vid)

Returns all the properties defined on a vertex.

graph_properties()

return a dict containing the graph properties/

Return type:

dict of {property_name:data}

has_vertex(vid)[source]

Tests whether a vertex belongs to the graph.

Parameters:

  • vid (int) - vertex id to test

Returns Type:

bool

index(vid)[source]

Index of a vertex

The Index of a vertex is a feature always defined and independent of time (like the index). It is represented by a non negative integer. The label of a vertex is the string defined by the concatenation of its class and its index. The label thus provides general information about a vertex and enables us to encode the plant components.

insert_parent(vtx_id, parent_id=None, **properties)[source]

Insert parent_id between vtx_id and its actual parent. Inherit of the complex of the parent of vtx_id.

Parameters:

  • vtx_id (int): a vertex identifier

  • parent_id (int): a vertex identifier

Returns:

Identifier of the inserted vertex (parent_id).

Returns Type:

int

insert_scale(inf_scale=None, partition=None, default_label=None, preserve_order=True)[source]

Add a scale to MTG

Parameters:

  • inf_scale (int) - New scale is inserted between inf_scale and inf_scale-1

  • partition (lambda v: bool) - Function defining new scale by quotienting vertices at inf_scale

  • default_label (str) - default label of inserted vertices

  • preserve_order (bool) - True iif children at new scale are ordered consistently

    with children at inf_scale

Returns:

MTG with inserted scale

Remark:

  • New scale is inserted in self as well.

  • function partition should return True at roots of subtrees where partition changes

and False elsewhere.

insert_sibling(vtx_id1, vtx_id2=None, **properties)[source]

Insert a sibling of vtk_id1. The vertex in inserted before vtx_id1.

Parameters:

  • vtx_id1 (int) : a vertex identifier

  • vtx_id2 (int) : the vertex to insert

Returns:

Identifier of the inserted vertex (vtx_id2)

Returns Type:

int

insert_sibling_tree(vid, tree)

Insert a tree before the vid. vid and the root of the tree are siblings. Complexity have to be O(1) if tree comes from the actual tree ( tree= self.sub_tree() )

Parameters:

  • vid – vertex identifier

  • tree – a rooted tree

is_leaf(vtx_id)

Test if vtx_id is a leaf.

Returns:

bool

is_valid()[source]

Tests the validity of the graph. Currently always returns True.

Returns Type:

bool

Todo:

Implement this function.

iter_edges(scale=-1)[source]
Parameters:

  • scale (int) - Scale at which to iterate.

Returns:

Iterator on the edges of the MTG at a given scale or on all edges if scale < 0.

Returns Type:

iter

iteredges(scale=-1)[source]

Iter on the edges of the tree.

label(vid)[source]

Label of a vertex.

Usage:
>>> g.label(v)
Parameters:

  • vid (int) : vertex of the MTG

Returns:

The class and Index of the vertex (str).

See also

MTG(), index(), class_name()

max_scale()[source]

Return the max scale identifier.

By convention, the mtg contains scales in \([0,max\_scale]\).

Usage:
>>> print g.max_scale()
Returns:

S, the maximum scale identifier.

Note

The complexity is \(O(n)\).

See also

scale(), scales()

nb_children(vtx_id)

returns the number of children

Parameters:

  • vtx_id: The vertex identifier.

Returns:

int

nb_components(vid)[source]

returns the number of components

Parameters:

  • vid: The vertex identifier.

Returns:

int

nb_scales()[source]
Returns:

The number of scales defined in the mtg..

Returns Type:

int

Note

The complexity is \(O(n)\).

nb_siblings(vtx_id)

returns the number of siblings

Returns:

int

nb_vertices(scale=-1)[source]

Returns the number of vertices.

Usage:
>>> g.nb_vertices()
100
>>> g.nb_vertices(scale=3)
68
Parameters:

  • scale (int) - Id of scale for which to count vertices.

Returns:

Number of vertices at scale or total number of vertices if scale < 0.

node(vid, klass=None)[source]

Return a node associated to the vertex vid.

It allows to access to the properties with an object oriented interface.

Example:

node = g.node(1)
print node.edge_type
print node.label
node.label = 'B'
print g.label(1)

print node.parent
print list(node.children)
order(v1)[source]

Order of a vertex in a graph.

The order of a vertex in a graph is the number of ‘+’ edges crossed when going from v1`to `v2.

If v2 is None, the order of v1 correspond to the order of v1 with respect to the root.

parent(vtx_id)

Return the parent of vtx_id.

Parameters:

  • vtx_id: The vertex identifier.

Returns:

vertex identifier

plot_property(prop, **kwds)[source]

Plot properties of MTG using matplotlib

Example:
>>> g.plot_property('length')
properties()

Returns all the property maps contain in the graph.

property(name)

Returns the property map between the vid and the data. :returns: dict of {vid:data}

property_names()

names of all property maps. Properties are defined only on vertices, even edge properties. return iter of names

property_names_iter()

iter on names of all property maps. Properties are defined only on vertices, even edge properties. return iter of names

reindex(mapping=None, copy=False)[source]

Assign a new identifier to each vertex.

This method assigns a new identifier to each vertex of the MTG. The mapping can be user defined or is implicit (mapping). This method modify the MTG in place or return a new MTG (copy).

Usage:

>>> g.reindex()
>>> g1 = g.reindex(copy=True)
>>> mymap = dict(zip(list(traversal.iter_mtg2(g,g.root)), range(len(g))))
>>> g2 = g.reindex(mapping=mymap, copy=True)
Optional Parameters:

  • mapping (dict): define a mapping between old and new vertex identifiers.

  • copy (bool) : modify the object in place or return a new MTG.

Returns:

  • a MTG

Background:

MTGs()

See also

sub_mtg()

remove_property(property_name)

Remove the property map called property_name from the graph.

remove_scale(scale)[source]

Remove all the vertices at a given scale.

The upper and lower scale are then connected.

Parameters:

  • scale : the scale that have to be removed

returns:

  • - g (the input MTG modified in place.)

  • - results (a list of dict) – all the vertices that have been removed

remove_tree(vtx_id)

Remove the sub tree rooted on vtx_id.

Returns:

bool

remove_vertex(vid, reparent_child=False)[source]

Remove a specified vertex of the graph and remove all the edges attached to it.

Parameters:

  • vid (int) : the id of the vertex to remove

  • reparent_child (bool) : reparent the children of vid to its parent.

Returns:

None

replace_parent(vtx_id, new_parent_id, **properties)[source]

Change the parent of vtx_id to new_parent_id. The new parent of vtx_id is new_parent_id. vtx_id and new_parent_id must have the same scale.

This function do not change the edge_type between vtx_id and its parent.

Inherit of the complex of the parent of vtx_id.

Parameters:

  • vtx_id (int): a vertex identifier

  • new_parent_id (int): a vertex identifier

Returns:

None

roots(scale=0)[source]

Returns a list of the roots of the tree graphs at a given scale.

In an MTG, the MTG root vertex, namely the vertex g.root, can be decomposed into several, non-connected, tree graphs at a given scale. This is for example the case of an MTG containing the description of several plants.

Usage:

roots = g.roots(scale=g.max_scale()

Returns:

list on vertex identifiers of root vertices at a given scale.

Returns Type:

list of vid

../_images/mtg_componentroots.png
roots_iter(scale=0)[source]

Returns an iterator of the roots of the tree graphs at a given scale.

In an MTG, the MTG root vertex, namely the vertex g.root, can be decomposed into several, non-connected, tree graphs at a given scale. This is for example the case of an MTG containing the description of several plants.

Usage:

roots = list(g.roots(scale=g.max_scale())

Returns:

iterator on vertex identifiers of root vertices at a given scale.

Returns Type:

iter

../_images/mtg_componentroots.png
scale(vid)[source]

Returns the scale of a vertex.

All vertices should belong to a given scale.

Usage:

g.scale(vid)
Parameters:

  • vid (int) - vertex identifier.

Returns:

The scale of the vertex. It is a positive int in [0,g.max_scale()].

scales()[source]

Return the different scales of the mtg.

Returns:

Iterator on scale identifiers (ints).

Note

The complexity is \(O(n)\).

scales_iter()[source]

Return the different scales of the mtg.

Returns:

Iterator on scale identifiers (ints).

Note

The complexity is \(O(n)\).

set_root(vtx_id)

Set the tree root.

Parameters:

vtx_id – The vertex identifier.

siblings(vtx_id)

returns an iterator of vtx_id siblings. vtx_id is not include in siblings.

Parameters:

  • vtx_id: The vertex identifier.

Returns:

iter of vertex identifier

siblings_iter(vtx_id)

returns an iterator of vtx_id siblings. vtx_id is not include in siblings.

Parameters:

  • vtx_id: The vertex identifier.

Returns:

iter of vertex identifier

sub_mtg(vtx_id, copy=True)[source]

Return the submtg rooted on vtx_id.

The induced sub mtg of the mtg are all the vertices which have vtx_id has a complex plus vtx_id.

Parameters:

  • vtx_id: A vertex of the original tree.

  • copy: If True, return a new tree holding the subtree. If False, the subtree is created using the original tree by deleting all vertices not in the subtree.

Returns:

A sub mtg of the mtg. If copy=True, a new MTG is returned. Else the sub mtg is created inplace by modifying the original tree.

sub_tree(vtx_id, copy=True)

Return the subtree rooted on vtx_id.

The induced subtree of the tree has the vertices in the ancestors of vtx_id.

Parameters:

  • vtx_id: A vertex of the original tree.

  • copy: If True, return a new tree holding the subtree. If False, the subtree is created using the original tree by deleting all vertices not in the subtree.

Returns:

A sub tree of the tree. If copy=True, a new Tree is returned. Else the subtree is created inplace by modifying the original tree.

vertices(scale=-1)[source]

Return a list of the vertices contained in an MTG.

The set of all vertices in the MTG is returned. Vertices from all scales are returned if no scale is given. Otherwise, it returns only the vertices of the given scale. The order of the elements in this array is not significant.

Usage:

g = MTG()
len(g) == len(list(g.vertices()))
for vid in g.vertices(scale=2):
    print g.class_name(vid)
Optional Parameters:

  • scale (int): used to select vertices at a given scale.

Returns:

Iterator on vertices at “scale” or on all vertices if scale < 0.

Returns Type:

list of vid

Background:

See also

children(), components(), vertices_iter()..

vertices_iter(scale=-1)[source]

Return an iterator of the vertices contained in an MTG.

The set of all vertices in the MTG is returned. Vertices from all scales are returned if no scale is given. Otherwise, it returns only the vertices of the given scale. The order of the elements in this array is not significant.

Usage:

g = MTG()
len(g) == len(list(g.vertices()))
for vid in g.vertices(scale=2):
    print g.class_name(vid)
Optional Parameters:

  • scale (int): used to select vertices at a given scale.

Returns:

Iterator on vertices at “scale” or on all vertices if scale < 0.

Returns Type:

iter of vid

Background:

See also

children(), components().

property root

Return the tree root.

Returns:

vertex identifier

openalea.mtg.mtg.simple_tree(tree, vtx_id, nb_children=3, nb_vertices=20)[source]

Generate and add a regular tree to an existing one at a given vertex.

Add a regular tree at a given vertex id position vtx_id. The length of the sub_tree is nb_vertices. Each new vertex has at most nb_children children.

Parameters:

  • tree: the tree thaat will be modified

  • vtx_id (id): vertex on which the sub tree will be added.

  • nb_children (int) : number of children that are added to each vertex

  • nb_vertices (int) : number of vertices to add

Returns:

The modified tree

Examples:
g = MTG()
vid = g.add_component(g.root)
simple_tree(g, vid, nb_children=2, nb_vertices=20)
print len(g) # 22

See also

random_tree(), random_mtg()

openalea.mtg.mtg.random_tree(mtg, root, nb_children=3, nb_vertices=20)[source]

Generate and add a random tree to an existing one.

Add a random sub tree at a given vertex id position root. The length of the sub_tree is nb_vertices. The number of children for each vertex is sampled according to nb_children distribution. If nb_children is an interger, the random distribution is uniform between [1, nb_children]. Otherwise, you can give your own discrete distribution sampling function.

Parameters:

  • mtg: the mtg to modified

  • root (id): vertex id on which the sub tree will be added.

Optional Parameters:

  • nb_vertices

  • nb_children : an int or a discrete distribution sampling function.

Returns:

The last added vid.

Examples:
g = MTG()
vid = g.add_component(g.root)
random_tree(g, vid, nb_children=2, nb_vertices=20)
print len(g) # 22

See also

simple_tree(), random_mtg()

openalea.mtg.mtg.random_mtg(tree, nb_scales)[source]

Convert a tree into an MTG of nb_scales.

Add a random sub tree at a given vertex id position root. The length of the sub_tree is nb_vertices. Each new vertex has at most nb_children children.

Parameters:

  • mtg: the mtg to modified

  • root (id): vertex id on which the sub tree will be added.

Returns:

The last added vid.

Examples:
g = MTG()
random_tree(g, g.root, nb_children=2, nb_vertices=20)
print len(g) # 21

See also

simple_tree(), random_tree()

openalea.mtg.mtg.colored_tree(tree, colors)[source]

Compute a mtg from a tree and the list of vertices to be quotiented.

Note

The tree has to be a real tree and not an MTG

Example:

from random import randint, sample
g = MTG()
random_tree(g, g.root, nb_vertices=200)

# At each scale, define the vertices which will define a complex
nb_scales=4
colors = {}
colors[3] = g.vertices()
colors[2] = random.sample(colors[3], randint(1,len(g)))
colors[2].sort()
if g.root not in colors[2]:
    colors[2].insert(0, g.root)
colors[1] = [g.root]

g, mapping = colored_tree(g, colors)
openalea.mtg.mtg.display_tree(tree, vid, tab='', labels={}, edge_type={})[source]

Display a tree structure.

openalea.mtg.mtg.display_mtg(mtg, vid)[source]

Display an MTG

..todo:: Write doc.

Download the source file ../../src/mtg/mtg.py.