2. The openalea.mtg.aml module: Long Tour¶
2.1. Reading the file¶
This page illustrates the usage of all the functionalities available in openalea.mtg.aml module. All
the examples uses the MTG file code_file2.mtg. If you are interested in the syntax, we stronly recommend
you to look at Section MTG file.
First, let us read the MTG file with the function MTG(). Note that only one MTG object can be manipulated at a time. This MTG object is the active MTG.
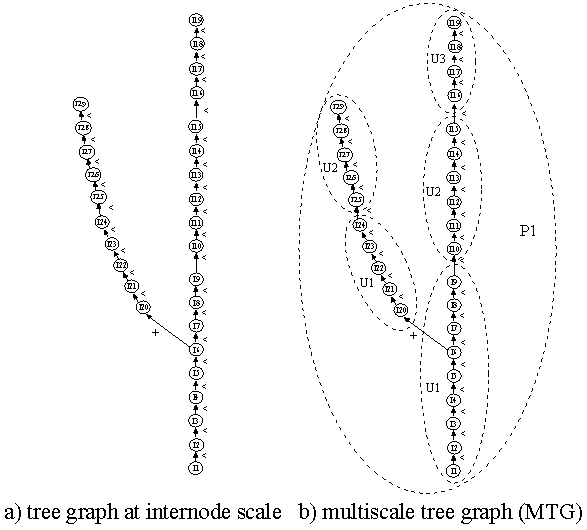
Figure 1: Graphical representation of the MTG file code_file2.mtg used as an input file to all examples contained in this page¶
>>> from openalea.mtg.aml import *
>>> g = MTG('user/code_file2.mtg')
>>> Active() == g
True
The Active() function checks that g is currently the active MTG.
If a new MTG file is read, it becomes the new active MTG object. However, the function Activate() can be use to switch between MTG objects as follows:
>>> h = MTG('user/agraf.mtg')
>>> Active() == h
True
>>> Activate(g)
>>> MTGRoot()
0
2.2. Feature functions¶
2.2.1. Order, Rank and Height¶
Order() (AlgOrder()) look at the number of + sign that need to be crossed before reaching the vertex considered
>>> Order(3)
0
>>> Order(14)
1
>>> AlgOrder(3,14)
1
Height() (AlgHeight()) look at the number of components between the root of the vertex’s branch and the vertex’s position.
>>> Height(3)
0
>>> Height(14)
10
>>> AlgHeight(3, 14)
10
Rank() (AlgRank()) returns the number < sign that need to be crosssed before reaching the vertex considered.
>>> Rank(3)
0
>>> Rank(14)
4
>>> AlgRank(3, 14)
5
2.2.2. Class(), Index(), Label(), Feature()¶
Class() gives the type of vertex usually defined by a letter
>>> Class(3)
'I'
and Index() gives the other part of the label
>>> Index(3)
1
When speaking about multiscale tree graph, we also want to access the Scale():
>>> Scale(3)
3
A new function called Label() combines the Class and Index:
>>> Label(3)
'I1'
Finally, Feature() returns value of a given feature coded in the MTG file.
>>> Feature(2, "Len")
10.0
2.2.3. ClassScale(), EdgeType(), Defined()¶
ClassScale() returns the Scale at which appears a given class of vertex:
>>> ClassScale('U')
3
EdgeType() returns the type of connection between two vertices (e.g., +, <)
>>> i=8; Class(i), Index(i)
('I', 6)
>>> i=9; Class(i), Index(i)
('U', 1)
>>> EdgeType(8,9)
'+'
Defined() tests whether a vertex’s id is present in the active MTG
>>> Defined(1)
True
>>> Defined(100000)
False
2.3. Date functions¶
The following function requires MTG files to contain Date information.
Todo
not yet implemented
Function |
|
|---|---|
DateSample(e1) |
|
FirstDefinedFeature(e1, e2) |
|
LastDefinedFeature(e1, e2) |
|
NextDate(e1) |
|
PreviousDate(e1) |
2.4. Functions for moving in MTGs¶
2.4.1. Trunk()¶
Trunk() returns the list of vertices constituting the bearing botanical axis of a branching system
>>> Trunk(2) # vertex 2 is U1 therefore the Trunk should return index related to U1, U2, U3
[2, 24, 31]
>>> Class(24), Index(24)
('U', 2)
>>> Trunk(3) # vertex 3 is an internode, so we get all internode of the axis containing vertex 3
[3, 4, 5, 6, 7, 8, 21, 22, 23, 25, 26, 27, 28, 29, 30, 32, 33, 34, 35]
>>> Class(35), Index(35)
('I', 19)
2.4.2. Father()¶
Topological father of a given vertex.
>>> Label(8)
'I6'
>>> Father(8)
7
>>> Label(9) # Let us look at vertex 9 (with the U1 label)
'U1'
>>> Father(9) # and look for its father's index
2
>>> Label(2) # and its father's label that appear to also be equal to 1
'U1'
2.4.3. Axis()¶
Axis() returns the vertices of the axis to which belongs a given vertex.
>>> [Label(x) for x in Axis(9)]
['U1', 'U2']
The scale may be specified
>>> [Label(x) for x in Axis(9, Scale=3)]
['I20', 'I21', 'I22', 'I23', 'I24', 'I25', 'I26', 'I27', 'I28', 'I29']
2.4.4. Ancestors()¶
Ancestors() returns a list of ancestors of a given vertex
>>> Ancestors(20) # of I29
[20, 19, 18, 17, 16, 14, 13, 12, 11, 10, 8, 7, 6, 5, 4, 3]
>>> [Class(x)+str(Index(x)) for x in Ancestors(20)]
['I29', 'I28', 'I27', 'I26', 'I25', 'I24', 'I23', 'I22', 'I21', 'I20', 'I6', 'I5', 'I4', 'I3', 'I2', 'I1']
2.4.5. Path()¶
The Path() returns a list of vertices defining the path between two vertices
>>> [Class(x)+str(Index(x)) for x in Path(8, 20)]
['I20', 'I21', 'I22', 'I23', 'I24', 'I25', 'I26', 'I27', 'I28', 'I29']
2.4.6. Sons()¶
In order to illustrate the Sons() function, let us consider the vertex 8
>>> Class(8), Index(8)
('I', 6)
>>> [Class(x)+str(Index(x)) for x in Sons(8)]
['I20', 'I7']
2.4.7. Descendants() and Ancestors()¶
Descendants() an array with all the vertices, at the same scale as v, that belong to the branching system starting at v:
>>> [Class(x)+str(Index(x)) for x in Descendants(8)]
Ancestors() contains the vertices on the path from v back to the root (in this order) and finishes by the tree root.:
>>> [Class(x)+str(Index(x)) for x in Ancestors(8)]
2.4.8. Predecessor() and Successor()¶
Predecessor() returns the Father of a vertex connected to it by a ‘<’ edge, and is therefore equivalent to:
Father(v, EdgeType-> ‘<’).
Similarly, Successor() is equivalent to
Sons(v, EdgeType=’<’)[0]
2.4.9. Root()¶
Root() returns root of the branching systenme containing a given vertex and therefore is equivalent to:
Ancestors(v, EdgeType=’<’)[-1]
>>> [Class(x)+str(Index(x)) for x in Ancestors(8)]
['I6', 'I5', 'I4', 'I3', 'I2', 'I1']
>>> Root(8)
3
>>> Class(3)+str(Index(3))
'I1'
Todo
Complex returns Scale(v)-1 why what is it for?
>>> Complex(8)
2
2.4.10. Components()¶
Returns a list of vertices that are included in the upper scale of the vertex’s id considered. The array is empty if the vertex has no components.
>>> Components(1, Scale=2)
[2, 9, 15, 24, 31]
>>> Components(1, Scale=3)
[3, 4, 5, 6, 7, 8, 21, 22, 23, 10, 11, 12, 13, 14, 16, 17, 18, 19, 20, 25, 26, 27, 28, 29, 30, 32, 33, 34, 35]
2.4.11. ComponentRoots()¶
Todo
to be done. find example
2.4.12. Location()¶
Vertex defining the father of a vertex with maximum scale.
>>> Label(9) # starting from a Component U1 at vertex's id 9
'U1'
>>> Father(9) # what is its Father ?
2
>>> Label(Father(9)) # answer: another U1 of vertex's id 2
'U1'
>>> Location(9) # what is the location of vertex 9
8
>>> Label(Location(9)) # the internode I6
'I6'
2.4.13. Extremities()¶
>>> Label(8)
'I6'
>>> Label(Extremities(8))
['I29', 'I19']
2.5. Geometric interpretation¶
Most of the following functions are not yet implemented. See Quick Start to manipulate MTGs to see the usage of PlantFrame() with dressing data.
You may also use the former AML code using openalea.aml package
2.5.1. PlantFrame() and Plot()¶
One can use openalea.aml for now:
>>> import openalea.aml as aml
>>> aml.MTG('code_file2.txt')
>>> pf = aml.PlantFrame(2)
>>> aml.Plot()
Shows the MTG file at scale 2. This is possible because Diameter and Lenmgth features are provided at that scale.
|
|
|
|
|
|
RelTopCoord(e1, e2) |
|
BottomCoord(e1, e2) |
|
RelBottomCoord(e1, e2) |
|
Coord(e1, e2) |
|
BottomDiameter(e1,e2) |
|
TopDiameter(e1,e2) |
|
Alpha(e1,e2) |
|
Beta(e1,e2) |
|
Length(e1,e2) |
|
VirtualPattern(e1) |
|
PDir(e1,e2) |
|
SDir(e1,e2) |
2.6. Comparison Functions¶
Todo
not yet implemented
TreeMatching(e1) MatchingExtract(e1)